Plato tells us that throughout his story of Atlantis, Greek names have been used to make it agreeable to his readers. Examples of these could be trireme for ship, hoplite for warrior, bulls for the animal used for sacrifice and the stade, which was a Greek unit of measurement intended to be a 1/10th of a minute of latitude. So the stade correspondingly measured according to Berriman (1953) 607.5 English feet or 185.166 metres. For the Greeks, the stade was simply 600 Greek feet, but related to English feet each Greek foot would have been 12.15 English inches (308.61 mm). There is a difference in the length of a foot between "Egyptian" feet, "Greek" feet and "Babylonian" feet because in each case they were derived from the latitude of the observer, Athens, Alexandria and Babylonia being at different latitudes would have slight differences in the length of the foot, whereas the English foot is based on a different system namely the division of the polar diameter of the planet which gives an invariable unit of 12 inches (304.8 mm) to the English foot.
If we could locate the actual plain of Atlantis, we could then measure it to see what size stade might have been used in comparison to Plato's Greek stade.
Ulf Richter (2005) wrote an excellent paper on Atlantis which he presented to the 2005 Milos conference. In it he speculates that the stade used in Atlantis might be a much smaller Egyptian unit called a "khet" of 172 feet (52.4 metres) which was 100 Egyptian Royal cubits.
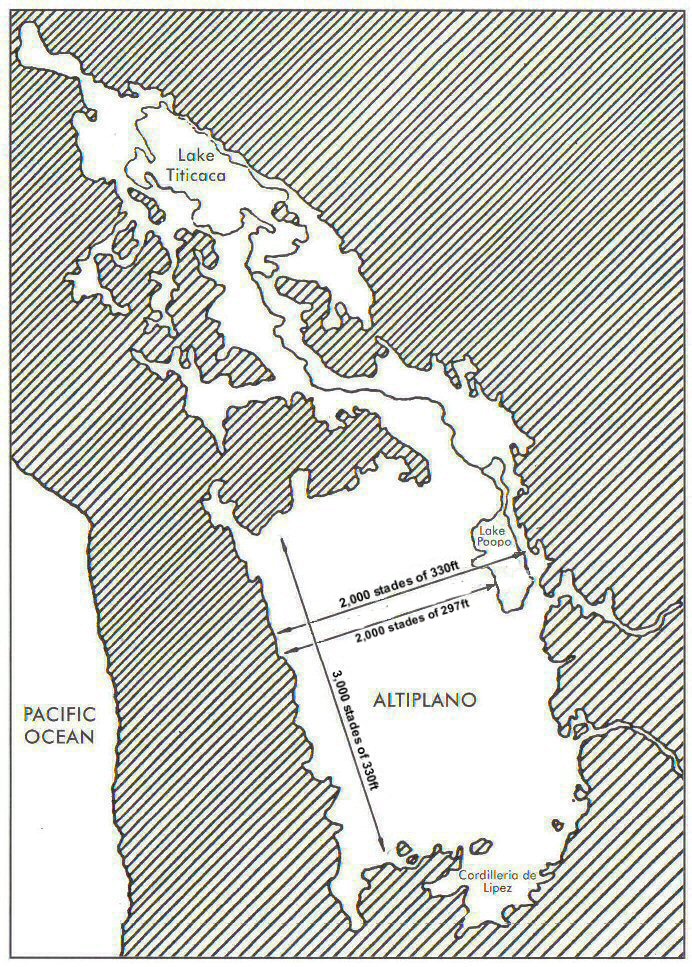
It is also clear that the word "stade" has been inserted inconsistently where different units might have actually have been used. From the dimensions of the rectangular plain found in Bolivia called the Altiplano which has been identified as the site of Atlantis, it is possible to measure it in the way Plato described - upwards from the sea (meaning Lake Poopo) and it measures 3,000 x 2000 "stades" of about 300 feet (92.5 metres), that is half a Greek stade and would be consistent with a unit which was a 1/20th of a minute of latitude. This would also fit in with South American systems of measurement since both the Mayans and Aztecs counted in 20's and the calendar at Tiwanaku (Bolivia) is also based on divisions of 20. The 300 foot stade is also the length of the base of the tower of Babylon, called a "furlong" by Herodotus, but today a furlong is 660 feet so what Herodotus found was a "half-furlong" or "half-stade". (see Herodotus, Histories, Book 1, 181) also since the 300 foot measurement was made by an English archaeologist of the mound in its ruined condition, the original may have been 297 feet which would have been the nearest unit in Sumerian or Babylonian measurements.
Since in measuring such a large area as the Altiplano it is difficult to establish the precise points exactly where the rectangular plain might have been measured from, it is equally possible that instead of an exact unit such as 300 English feet, the stade could have been half a geographic stade making it 303.75 feet (92.583 metres) or if it were set out in Sumerian units it could have been a stade of 297 feet (90.525 metres) which would have been 180 Sumerian cubits, or it could have been a stade of 330 feet (100.584 metres)making it half a furlong i.e. 200 sumerian cubits.



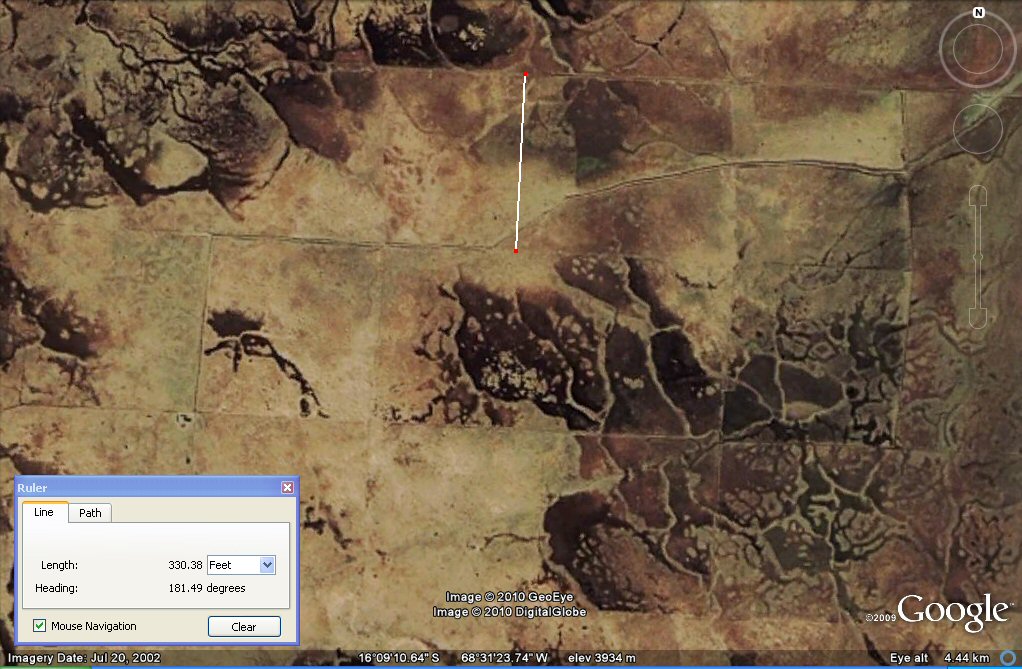
Above, measuring from the edge of the sea to the 12,000ft contour on the western side suggests a stade of 297ft
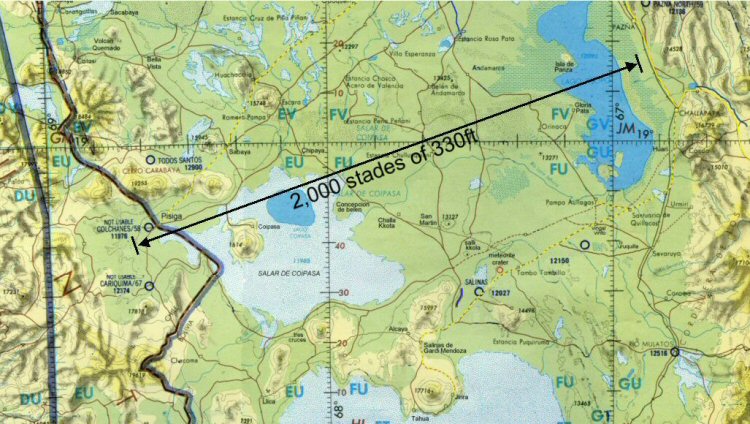
Above, measuring the full width of the plain including the sea to the 12,000ft
contour suggests a stade of 330ft
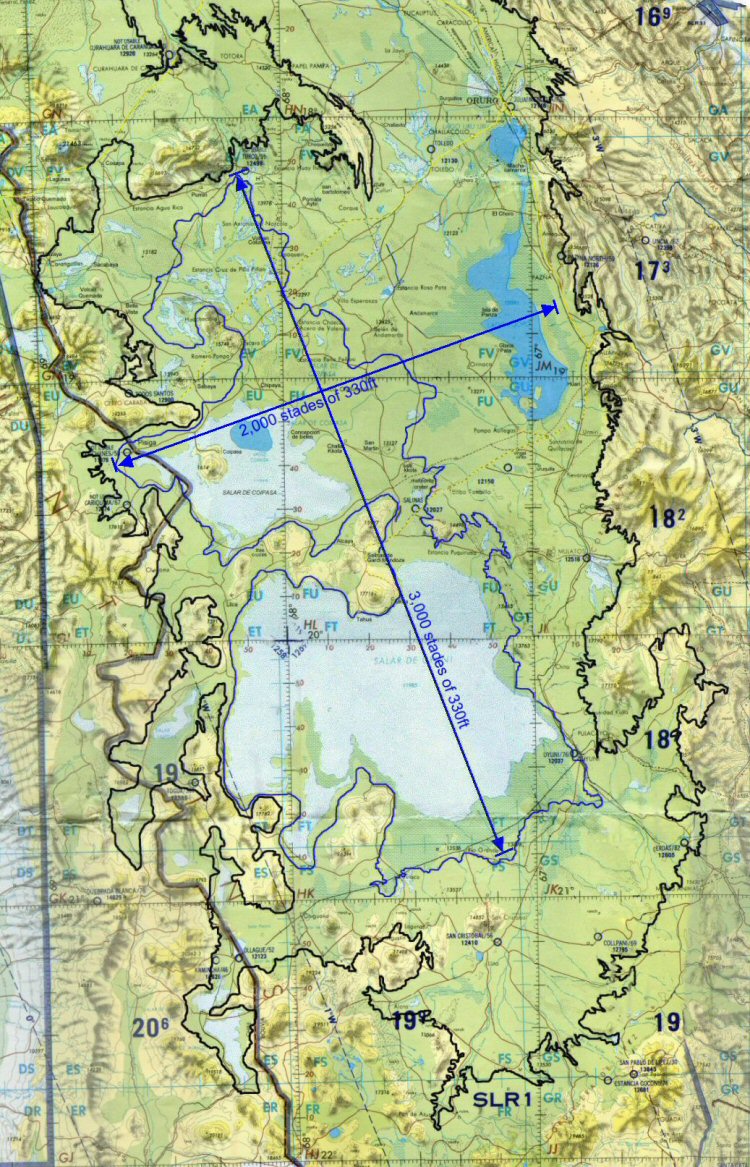
Above, The stade of 330ft fits better as the length of the plain from where
it meets the 12,000ft contour (coloured blue) at its northern edge to where it meets
the 12,000ft contour on the southern edge of the Salar de Uyuni with the width of the
plain shown here from the 12,000ft contour on its western side to where it meets the
mountains on the eastern side, thus defining it as 3,000 x 2,000 stades.
In the case of the circular formation found at Pampa Aullagas, the "best fit" for the zones of canals has been found to be a stade of 165 feet (50.3 metres) which is also an ancient Sumerian unit of measurement and similar to the 172ft "khet" proposed by Ulf Richter.
The plain was quoted by Plato to contain 60,000 allotments of 10 x 10 stades and in this respect using the 330ft Sumerian stade there would be as Plato said, 60,000 "allotments" separated by canals at intervals of 100 stades of 330ft.
A system of parallel canals which measure about 5 feet (1.5 metres) wide similar to those described by Plato has been found on the Altiplano in this area using high resolution satellite photos
A section of giant channel has been found to the west of Lake Poopo and two sections of giant canal 200 feet wide (60 metres) have also been found near Oruro and it is hoped that archaeological field work can be undertaken in this area to establish dating. Due to insufficient high resolution coverage, it is not possible to study the entire area where the canals exist including to the west of Lake Poopo but sufficient coverage exists to demonstrate the existence of this parallel canal system in an area which is now mostly salt desert.
A similar network of straight canals about this width has also been found covering a large area of the Beni region of Bolivia, where they run between mounds which were used for habitations and also connected by causeways which run alongside the canals.
The satellite imagery made freely available by Google Earth allows us to undertake searches for similar canal networks in other areas of the Americas.
The oldest civilisation of meso-America is said to be that of the Olmecs, thought to have arrived there around 1500 to 1200 BC.
Satellite images show that the area around Tabasco was previously covered in an extensive system of canalised irrigation in what is now swamp and lagoon covered land

above, plots of the Olmecs/Mayas in the Tabasco region of Mexico.
At first it is sometimes difficult to distinguish between ancient and modern canalisation or old canals which have been re-used in modern times or sometimes even routes of old canals which have been used as roads or paths, but archaeological studies done in this area confirm the existence of ancient canals.
In this zone of established ancient canals we can identify canals forming a grid pattern similar to that mentioned by Plato for Atlantis and using the satellite we can measure the size of the plots or "Allotments".
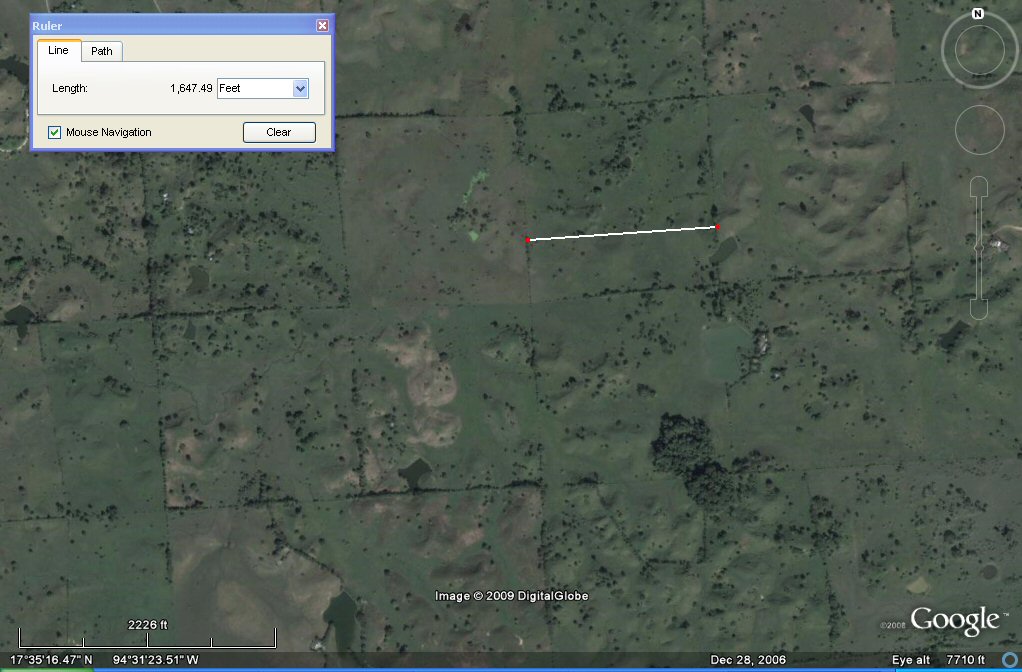
above, plots approximate to 1650 feet or 100 stades of 165 feet.
These plots seem to be set out on average in blocks of 1650 feet (502.92 metres). This means that each side would be 10 Sumerian "stades" of 165 feet such as found for the circular complex of the Atlantis site at Pampa Aullagas. Each side would also measure 1,000 "Sumerian cubits of 19.8" (502.92 mm).
This is consistent with Plato's description that in Atlantis, the size of the allotment was 10 x 10 stades, but here we have the same problem that perhaps the ancient translators had - what to actually call the units because "Stade" was used to describe the unit measuring the plain of Atlantis which in fact was most probably a double-unit of 330 feet, whereas this smaller "stade" of 165 feet is similar to the Egyptian unit called "khet" except that it measured 100 Sumerian cubits instead of Egyptian cubits. (150 Sumerian feet ) [50.292 metres].
This is additionally consistent with the size of a plot of land in ancient Egyptian times which was based on the Egyptian unit called "khet" which measured 100 cubits and a square area called "setat" which was 1 khet x 1 khet makng 100 x 100 cubits.
In Egypt the standard award of a plot of land consisted in 10 "setat" usually in the form of a strip of land 100 cubits wide by 1,000 cubits long called "a thousand of land" whereas warriors were usually awarded 12 "setat" which Herodotus (II,168) called 12 "arurae".


A UK allotment was originally 10 poles of 16.5ft x 1 pole of 16.5ft ie. 165ft x 16.5ft (100 Sumerian cubits x 10 Sumerian cubits = 1,000 sq. cubits) and today the equivalent is 250 sq metres, said to be enough to feed a family of 4. But according to Berriman, a landholder's award was 10 setat = 100,000 sq. cubits.

There was also a relationship between the Sumerian and the Egyptian cubits in the ratio of 24/25 so the Sumerian cubit of 19.8" was 24/25ths of the Egyptian cubit of 20.625".
The blocks which contain "warriors land" are set out in sides of relationship 5 to 6, or 10 to 12 and no doubt other variations were possible as the principal blocks could also have been divided by 8 or 4 resulting in irregular shapes, but the principal unit as described by Plato was the 10 x 10 block such as the example found in the Tabasco area.

above, this block in Tres Zapotes, Veracruz, Mexico
measures 1650 feet
wide so is 1000 Sumerian cubits square and is divided into strips of 200
x 1000 cubits i.e. 330ft wide, which would also be 96 x 480 Mayan
hunabs.

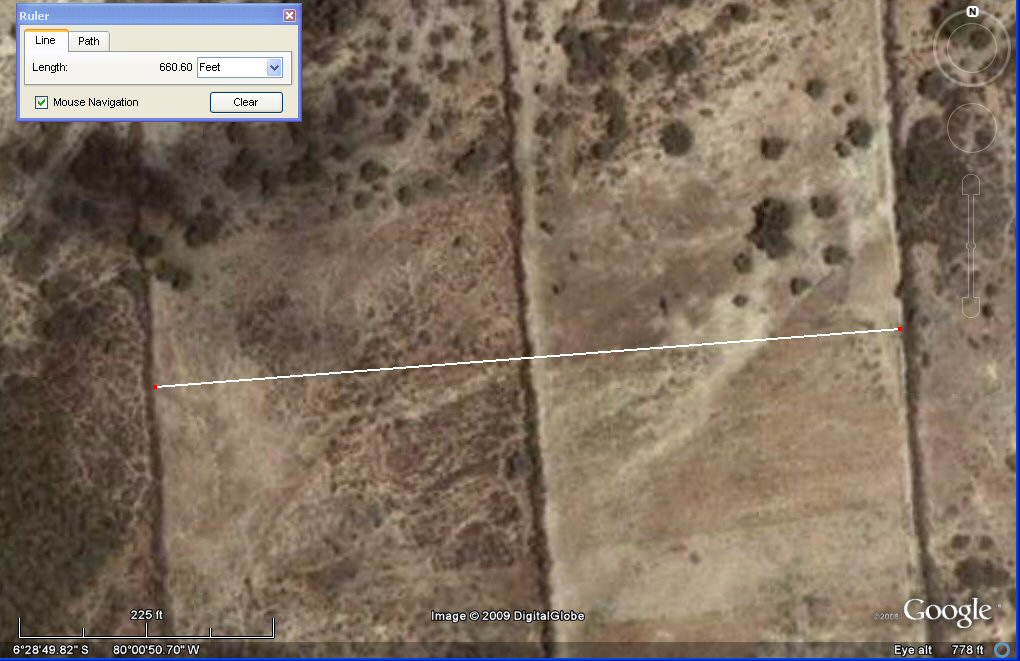
above, these adjacent plots near Tucume, Peru are 330
feet wide which is
200 cubits of 19.8" or 2 stades or khet of 165 feet or 1 stade of 330ft
as used to describe the length and breadth of the Altiplano.
above, these adjacent plots near Tucume, Peru have combined width of 660 feet which
is 400 cubits of 19.8" or 4 stades or khet of 165 feet or 2 stades of 330ft as used to describe the Bolivian altiplano or
1 x standard "Sumerian" furlong.

above, these 2 x adjacent plots near Tucume, Peru are
2400 cubits of 19.8" long making
them 12 x 330ft stades of the type used to describe the Bolivian
altiplano long x 1 stade of 330ft wide i.e each
is the length of a "warrior plot" and snce the two plots have a
combined width of 400 cubits or 1 furlong, the total area is 8 x
"warriors plots".
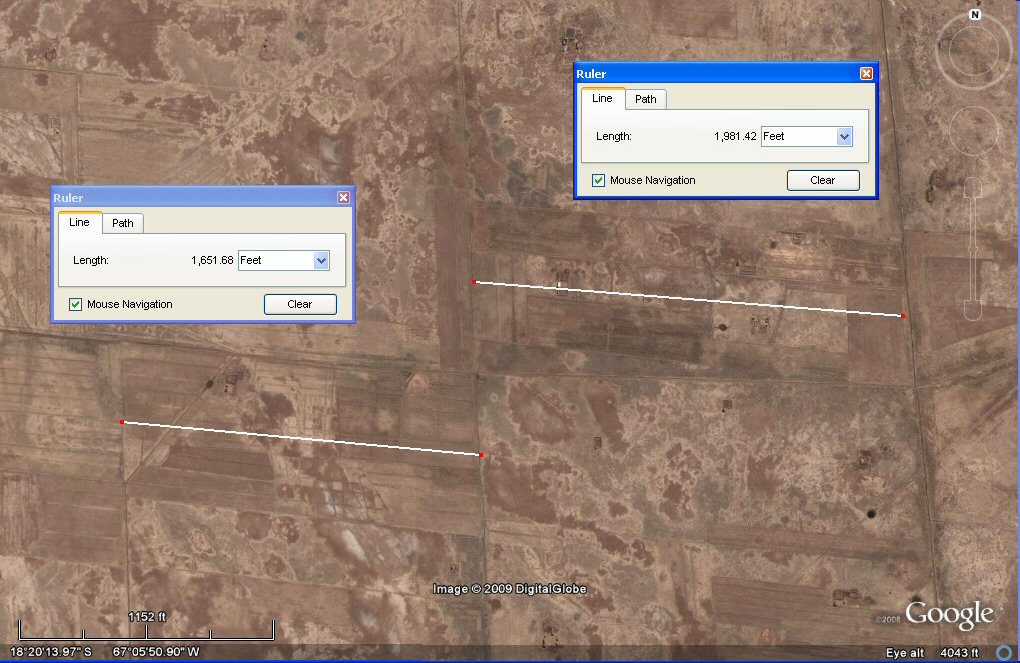
above, these adjacent plots on the Altiplano are 1650 and 1980 feet long respectively,
making the one on the left equal to 1000 cubits and the one
on the right 1200 cubits therefore equal in length to "standard" Atlantis plot and the "warriors plot" mentioned above.
regular blocks of 10 x 10 stades or khet of 165 feet in the Tabasco
area of Mexico, each block is 1000 x 1000 cubits. Four of these squares would make the allotment of
10 x 10 stades of 330ft in terms of the stade describing the length and breadth of the rectangular Altiplano.

Above,These channels on the Bolivian Altiplano
in the Tiwanaku/La Paz region are 1 x furlong apart making them
at intervals of 660ft which is 2 x the 330ft "stade" found measuring
the rectangular plain and 4 x the 165ft stade found at Pampa Aullagas and in Mexico.

At last the Altiplano gives up its secrets! These channels
on the Bolivian Altiplano north of Peñas which is north west of La Paz region are in regular plots
of 330ft confirming the use of the 330ft stade to describe the rectangular plain next to Lake Poopo.
In most regions, the underlying system of regular canals
in straight lines has disappeared, but in this region north of Penas
remains of these channels at 330 ft intervals can be clearly seen.
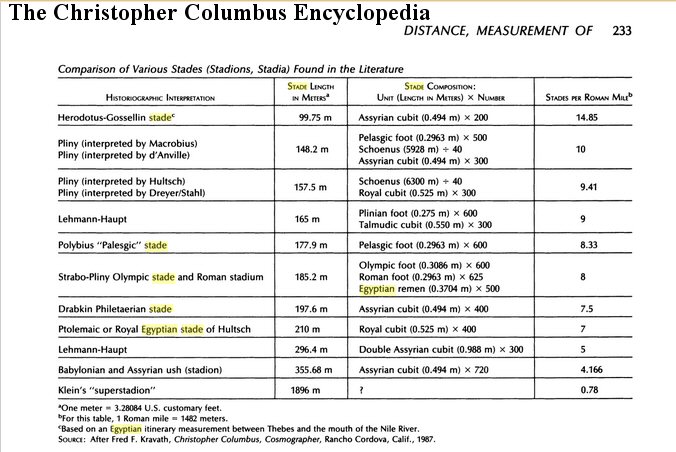
above, A stades chart from "The Christopher Columbus Encyclopedia" shows an Assyrian stade of 200 cubits,
so not unreasonable that the Atlantis stade used to measure the Plain should also be 200 cubits.

In the above composite photos, the thin white grid lines
are aligned to present day true North as provided by Google Earth.
The canals are aligned to just east of North and just south of East and
are of the same alignment as the pyramid of Akapana at Tiwanaku.
The significance, setting aside Atlantis for the moment, is that the
plots being in units
of half furlong and one furlong, when dated positively to before the
Conquest,
prove conclusively a contact between the Americas and the "Old World"
long before Columbus.

the above earthwork in Brasil measures 200 Sumerian cubits wide.....
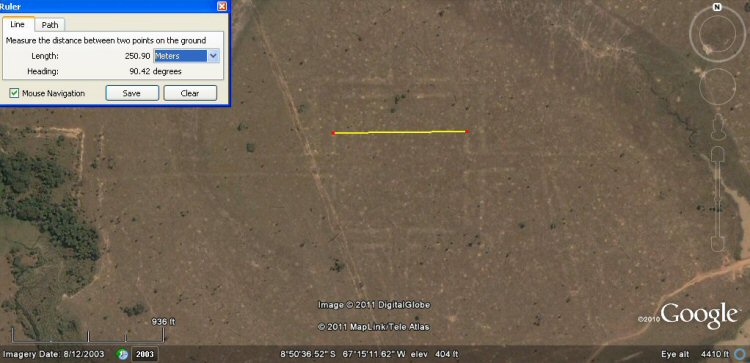
the above earthwork in Brasil measures 500 Sumerian cubits wide.....

above, the Puma Punka in Tiwanaku measured 500 sumerian feet or 100 sumerian double yards wide.....
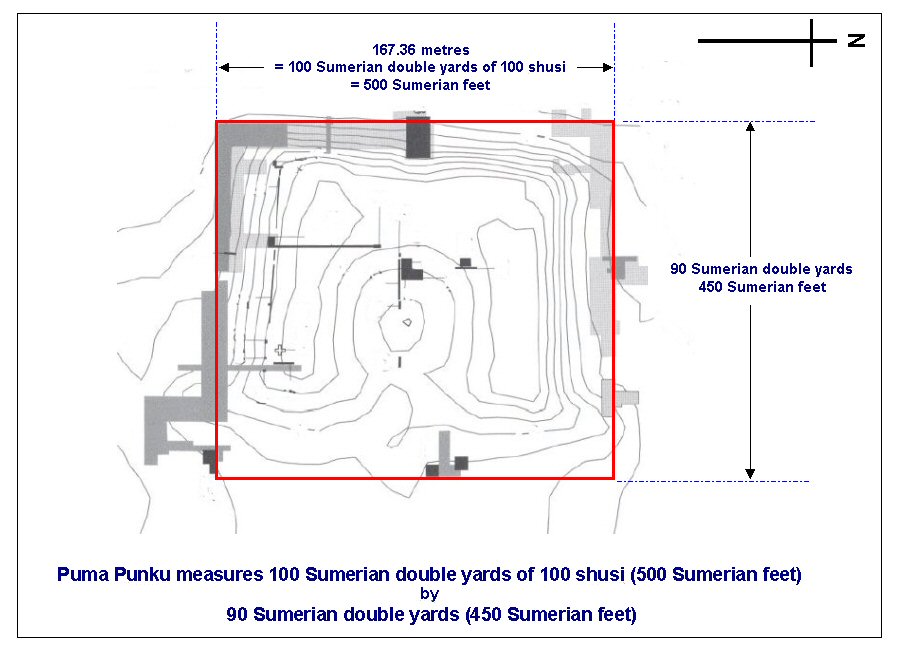
Above, the Puma Punka in Tiwanaku measured 500 x 450 Sumerian feet.....

Above, in this zone south-east of Peñas an underlaying system of canals forms a chequerboard pattern with squares of
600 sumerian cubits or
300 metres.
Above, these underlaying canals form blocks of 600
Sumerian cubits or 300 metres. It can be seen on this photo where older
canals have been redug in modern times.
The metre was adopted by the French academy of Sciences
for universal use in 1793, so if these canals are more recent than 1793,
or are modern, they could have been
set out in metres, however if they are pre-Columbian then they are
probably set out in "Sumerian" cubits of 19.8" whilst if they date from
after
the time of the Spanish Conquest they could still be in "Sumerian"
units such as cubits and furlongs since these were also brought over by
the Spanish as the old Spanish vara was in fact the "Sumerian" yard of
33.0". Each block is 600 Sumerian cubits or 360 Sumerian yards square.

Above, the underlaying canals form blocks of 600 Sumerian cubits, 360 sumerian yards or 300 metres.
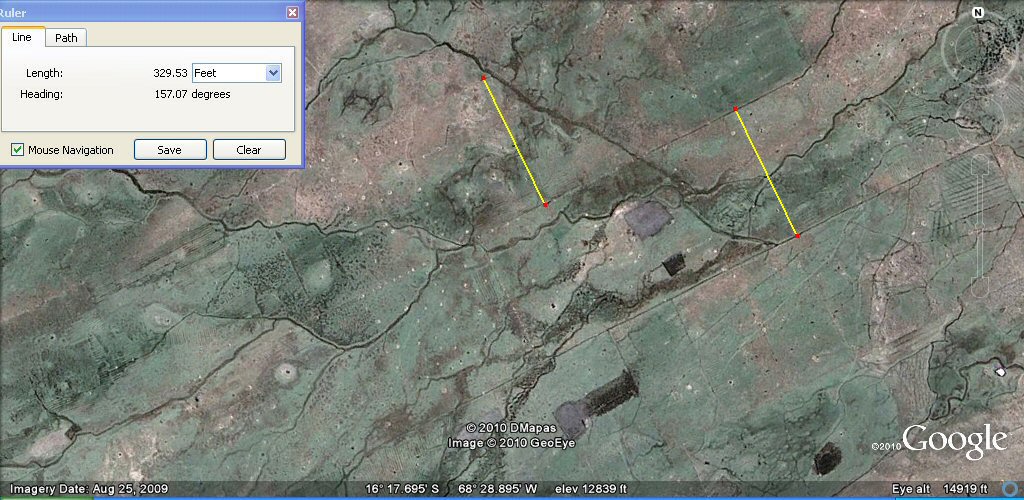
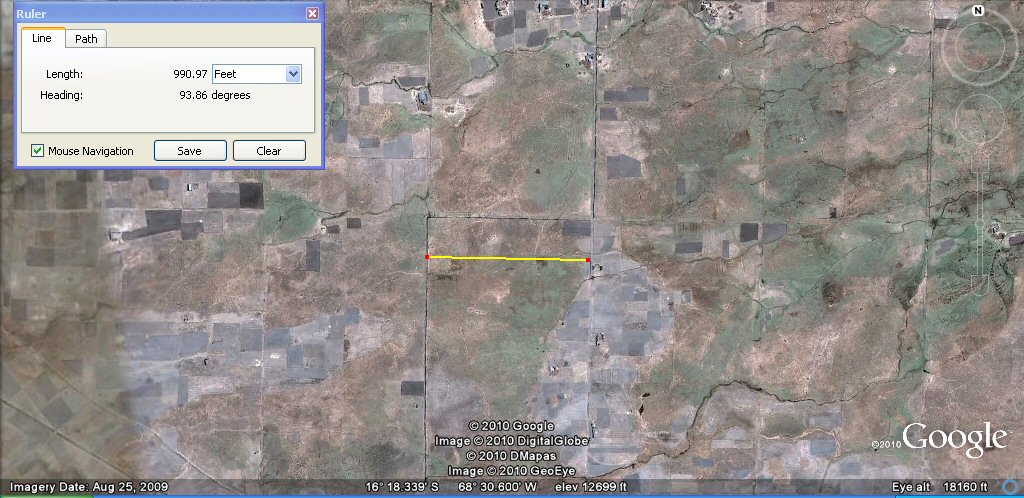
Above, these channels are about 330 feet (half furlong or 200 Sumerian cubits) or 100 metres
apart as measured by the yellow lines.
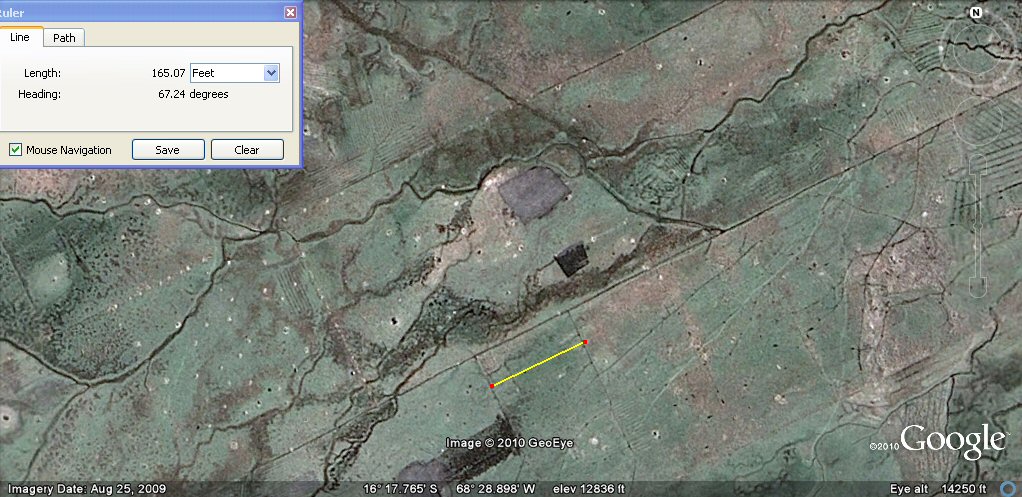
Above, in the same area, these sub-channels are about 165 feet (100 Sumerian cubits) or 50 metres
apart as measured by the yellow line. On the one photo it can be seen how basic units such
as a "stade" of 100 cubits (165ft) were doubled to give another "stade" of 200 cubits (330ft) and with
other multiples such as
400 cubits (660ft or 1 furlong) and 600 cubits (990ft). If these canals are pre-Columbian then they show the use of "Sumerian"
measurement units in the Americas.
If they are of more
recent times, then they did not last long and in any event show how easily the canals wash away
and disappear over time....
Measuring the width of the rectangular plain from the edge of the sea suggested a stade of 297ft and we can compare this unit to a stade of 330ft obtained by measuring the overall width of the plain.

Proportionately, each of Plato's allotments of 10 x 10 stades using stades of 297ft would enclose 18 x 18 setat of 100 x 100 cubits with divisions into landholder's strips of 10 "Atlantean" setat making 6.25 acres (2.75 hectares) per landholder or "warriors" strips of 12 setat making 7.5 acres or 3 hectares per warrior. With each allotment containing 18 x 18 or 324 setat, they would accommodate 32.4 standard landholders, or could be more conveniently divided into 18 landholder's strips of 10 setat plus 12 warriors strips of 12 setat, though in practice land was usually allocated on the basis of needs per family with multiples of the fundamental unit of 1 setat of 100 x 100 cubits being a useful basic measure for allocation.
However, if the stade were the 330ft half-furlong, then, each of Plato's allotments of 10 x 10 stades
using stades of 330ft would enclose 20 x 20 setat of 100 x 100 cubits (similar to the division of Time
into 20 x 20 months in the Tiwanaku calendar) with divisions into 20 rows of 2 x landholder's strips
of 10 "Atlantean" setat making 6.25 acres (2.75 hectares) per landholder with a convenient round number
of 40 landholders or families per allotment which could also be divided into quarters with 10 landholders
or families per quarter - and after all, under Inca rule, the whole country was called "Tahuantinsuyo"
and similarly divided into four quarters.

According to Plato, the Atlantis plain measured 3,000 x 2,000 stades: the distance between the principal canals on the Atlantean plain was 100 stades, and the allotments were 10 x 10 stades so if each "stade" were 297ft the distance between major canals would be 29,700ft whereas using the 330ft stade 330ft the distance between major canals would be 33,000ft, in both cases forming divisions which each contain 100 allotments and there would still be 60,000 allotments all told. With major canals at 100 stade (of 297ft) intervals, each division between the major canals could contain 10 x 10 allotments of 10 x 10 stades of 297ft or 18 x 18 blocks of 10 x 10 khet of 165ft and each block of 10 x 10 khet (1000 x 1000 cubits) supported 10 x landholder strips of 10 setat so either way, the square division between major canals would support 324 landholder plots or familes subdivided into "allotments" of 32.4 familes if standard plots of 10 setat were used.
Alternatively with major canals at 100 stade (of 330ft) intervals, each division between the major canals could contain 10 x 10 allotments of 10 x 10 stades of 330ft or 20 x 20 blocks of 10 x 10 khet of 165ft and each block of 10 x 10 khet (1000 x 1000 cubits) supported 10 x landholder strips of 10 setat so the square division between major canals would support 400 landholder plots or families with each quarter division supporting 100 landholders or familes if the standard 10 setat plot were used.
The division of land into blocks of 10 x 10 khet would be consistent with Inca numerical systems which were decimal and each block of 10 x 10 khet would have contained 10 landholder strips of 10 setat, each of 100 x 100 cubits - under the Inca system, ten workers had a "straw boss" and ten of these groups had a foreman and so on.
So ultimately, it would seem that the "Atlantis" stade used to describe the Plain was a half-furlong of 330ft, and this unit in turn was divided by 2 to give a smaller "stade" or "khet" of 100 "Sumerian" cubits (165ft) which formed the basis of parcels for land distribution.
Inca political organisation ...


Plato's atlantis was likewise divided into 10 kingdoms ...
Appendix 1
Looking at the following chart we can see why Plato said the numbers 5 and 6 did "honour to the odd and even".
Taking the circumference of the world as 360º, each degree comprises 60 "geographic" or "nautical" miles. We can then choose to divide the geographic mile by 6,000 for geographic feet, or by 5,000 for Egyptian remen.
But first, we have four different ways to calculate the geographic mile. We could take the polar diameter x p and divide by 360 x 60. Or we could take the equatorial diameter x p divided by 360 x 60.
There again we could take a minute of latitude of where we lived and use that as our geographic mile which would vary depending on whether we lived in Greece, Athens or Babylonia, or alternatively, for a more Universal geographic mile we could take the mean figure for a minute of latitude and use that.
The Greeks to calculate the Greek mile or geographic mile used a minute of latitude in Greece then divide by 6,000 to find the length of the "Greek foot".
In Egypt on the other hand, they took the mean figure for a geographic mile then divided this distance by 5,000 and called this distance 1 x remen. From the base of a square of 5,000 remen of 14.58", (one geographic mile) they obtained a diagonal which became 5,000 Egyptian Royal Cubits of 20.625".
This was very useful for land surveying since in order to set out a square of 100 royal cubits, all they had to do was to set out a base line of 200 remen and intersect two arcs of 100 royal cubits on one side of the base line, and intersect 2 arcs of 100 royal cubits on the other side of the base line to form a perfect square.
The Egyptian royal cubit comprised 28 fingers which was 7 palms, whereas 6 palms or 24 fingers made the regular Egyptian cubit and 4 palms or 16 fingers made the Egyptian foot.
If you set out a square whose sides were 2400 Egyptian royal cubits of 20.625", and then divided by 2500 you would then have units of Sumerian cubits of 19.8". Interestingly enough, a rectangle whose base length was 600 Sumerian feet of 13.2" and whose side is 500 Sumerian feet of 13.2", will also have a diagonal of 500 Egyptian royal cubits of 20.62".
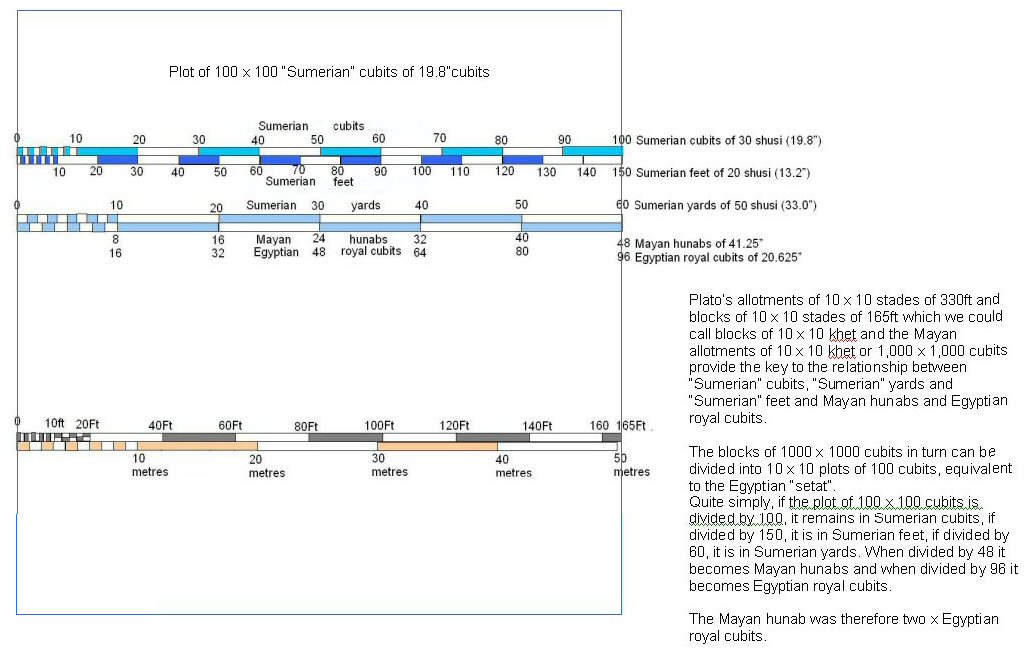
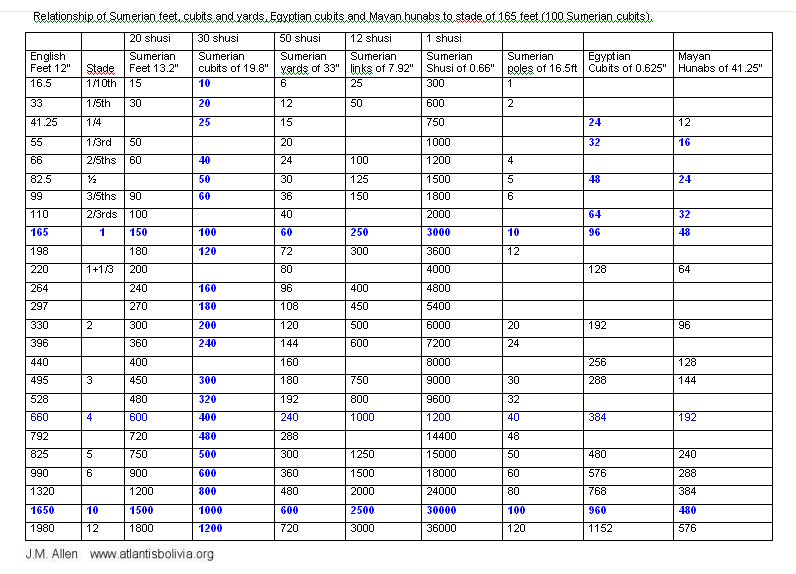
100 Egyptian royal cubits made an Egyptian unit called a "khet" while 100 Sumerian cubits make what we might call an "Atlantean" or "Olmec" stade which correspondingly comprised 100 Sumerian cubits, 150 Sumerian feet, 60 Sumerian yards, or 30 Sumerian double-yards of 100 Sumerian shusi - if you divided it by thirds you had 50 Sumerian feet and two thirds were 100 Sumerian feet while if you divided it by 96 it became 96 Egyptian royal cubits or dividing by 48 gave Mayan hunabs so 1 x Mayan hunab was 2 x Egyptian royal cubits.
2 x Atlantean stades of 165 feet made an Atlantean stade of 330 feet, and 2 x the 330ft stade made the furlong of 660ft which was 600 Sumerian feet….
The differences arose depending on your preferred mathematical method, whether you divided by halves, quarters or eighths or by thirds while the Babylonians/Sumerians generally preferred 60's, the Egyptians 10's and the Mayans 20's ….

Above, chart showing the origins and divisions of the respective measurement systems.
Rulers of 300mm exist in the British Museum in London where the Egyptian foot was divided into 16 fingers; 24 fingers made a geographic cubit and 28 fingers made the royal cubit of 525mm. In other words, the royal cubit contained an extra palm compared to the geographic cubit.
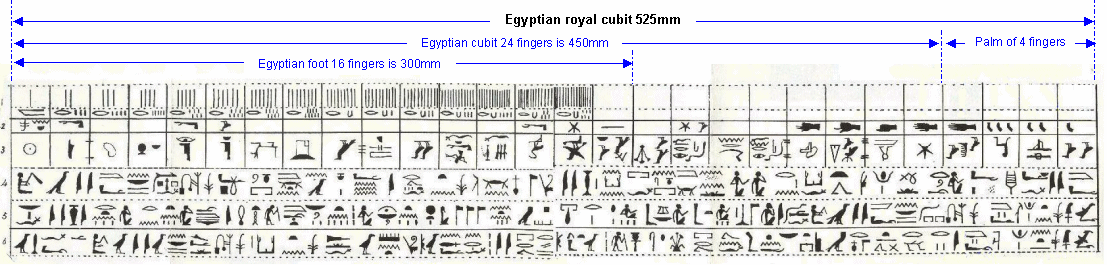
Above, Egyptian royal cubit rule of 525mm (20.67 inches) divided into 28 fingers.
Another value of Egyptian Royal cubit was 20.625" where this cubit was the diagonal of a square whose sides were a unit called a "remen" of 14.58" which was a 1/5000th part of a minute of latitude. This is the cubit built into the sides of the Great Pyramid in Egypt whose sides measure 440 such cubits. 24/25ths of this cubit would be 19.8" which is the Sumerian cubit of 30 shusi. And 10 "loka"of 600mm are virtually 12 Sumerian cubits of 19.8" making it difficult to determine which units really were used at Tiwanaku.
The Sumerian units were [16]
Shusi of 0.66"
Link of 12 shusi (7.92")
Foot of 20 shusi (13.2")
Cubit of 30 shusi (19.8")
Yard of 50 shusi (33.0")
Double yard of 100 shusi (66.0")
Pole of 16.5ft (15 Sumerian feet)
Furlong of 660ft (600 sumerian feet) etc.

Above, the shusi of 0.66" according to Berriman. [16]
For those who are curious as to why there should be two different lengths of Egyptian Royal Cubit, I will give the explanation here. When at the time of the French revolution they attempted to survey the circumference of the Earth to give a standard unit of measurement, they defined the average circumference as 40,000,000 metres, this was the origin of the unit called the metre. Today's figure for the average circumference is 40,008,258 metres. Alternative methods of measuring the circumference of the Earth would be to measure it at the equator, where it is largest, or to measure it through a meridian, which is a line passing North to South through both north and south poles.

Above, the latest measurements of the equator and polar meridians from Wikipedia.
When the Egyptians or whoever it was calculated the length of the Royal Cubit, they obtained one value by measuring from the meridians and the other value by measuring from the equator. Instead of dividing the circumference into 40,000,000 to obtain a metre, they divided the equatorial circumference by 360 then by 60 to obtain a geographic mile. They then divided this by 5,000 to obtain a unit called a "remen" which became the sides of a square whose diagonal was one cubit - in this case the "royal cubit" of 525mm.
For an alternative cubit for land surveying, they could take the average nautical mile of 6076.884ft, or the meridian mile as defined above of 6076.82ft, divide this by 5000 gives a remen of 14.584" which becomes the sides of a square and gives a corresponding diagonal for the square as 20.625" royal cubit with 24/25ths of this Egyptian Royal Cubit being the Sumerian cubit of 19.80". This cubit when made the diameter of a wheel measured out a distance of 66" - the Sumerian double yard of 100 Sumerian shusi and land plots of 100 Sumerian cubits of 19.8" were equivalent to 96 Egyptian cubits of 20.625" - all very practical for land surveying and subdivision.In the time of the Inca, the Empire was divided into four quarters and the country known as "The Land of the Four Quarters". When we think of the modern metre, the circumference of the globe was theoretically divided into 40,000,000 parts to obtain the value of the metre, and this meant that correspondingly, each quadrant was divided into 10,000,000 metres. What if the ancient Tiwanakotas divided the quadrant not into 360 in the manner of the Egyptians and Babylonians, but counting in 20's, divided by 20,000,000? Then they would obtain a cubit of 500 mm (19.685") and could even further subdivide by 20 giving an "inch" of 25 mm and this in turn could be divided by 20 giving "lines" of 1.25mm so a "loka" of 600 mm would be 24 "inches" of 24 mm or 480 "lines", an Egyptian cubit of 525 mm would be 420 "lines" an Egyptian geographic cubit of 450 mm would be 360 "lines" and an Egyptian foot of 300 mm would be 240 "lines". The Egyptian cubit of 525 mm was ordinarily divided by 28 to give a digit of 18.75 mm, but if we calculate in "lines", then it would be 15 "lines"... The English inch, as we call it, was obtained not from the circumference of the globe, but from the diameter which was divided firstly by 1,000,000,000 to obtain a "half-inch", then this unit was doubled to give the English inch, or alternatively we could think of it as the polar radius divided by 500,000,000 - this in turn could also be divided by 20,000,000 to give a "sacred cubit" of 25".
Edmund Kiss published (1937) in a book on Tiwanaku some dimensioned plans of additional temples in Tiwanku and these suggest the cubit of 19.68" was also used there, but once again, lack of available, accurate data means that at this stage we can only offer these cubit variations as possibilities to be borne in mind.
Appendix 2
Evidence of "Sumerian" cubits of 19.8" and "Egyptian" cubits of 20.625" at the city of Ur or Uru in Chaldea
*The city known as "Ur" by some archaeologists is also known by the name of "Uru" according to French archaeologist G. Maspero.

Above, frontispiece, History of Egypt, Chaldea, Syria, Babylonia and Assyria

Above, map showing the location of Ur also called "Uru"



Above, The lower storey 198 feet in length was therefore 120 x "Sumerian" cubits of 19.8" (180 Sumerian feet) and its width was 100 x "Egyptian" cubits of 20.625". The height of 20ft was probably 19.8ft making 1 x "gar" of 12 x "Sumerian" cubits of 19.8", however the tower at Babylon has been reported with stages at intervals of 20ft, the difference is so small as to be difficult to measure in a ruined building. A plinth 7ft high would be 4 x Egyptian Royal Cubits of 20.625"
Therefore both "Sumerian" cubits and "Egyptian" cubits were present in this building confirming the existence of the dual system found at Teotihuacan, Mexico,

Above, early drawing of the temple at Uru (UR) from Maspero's book.

Above, more modern interpretation of what the temple looked like at Uru (UR).
Tiwanaku cubits
Click here for Tiwanaku cubits
Tiwanaku calendar
Click here for Tiwanaku calendar
For measured intervals between Altiplano canals,
click HERE
Teotihuacan measuring unit
Click here for Teotihuacan measuring unit
Teotihuacan measuring unit at the citadel
Click here for citadel cubits Teotihuacan measuring units
Chichen Itza and El Castillo cubits
Click here for Chichen Itza and El Castillo cubits
Monte Alban cubits measuring units
Click here for Monte alban, measuring units
Jim Allen, 6 June 2009, updated 10th April 2010 and 10th Jan 2011
email webatlantis@hotmail.com