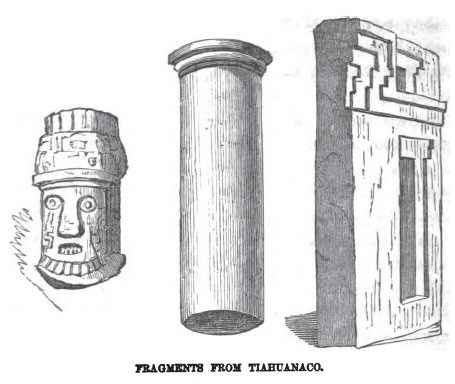
Above, Tiwanaku pillar by George Squier 1851
DECODING THE QUIPU
mathematical system
and Yupana
by Jim Allen
Background
I remember reading Guaman Poma's book "Letter to a King" in the modern version by Christopher
Dilke (based upon "El primer nueva corónica [sic] y buen gobierno" (The First New Chronicle and Good Government)
and studying the various original drawings of life in the time of the Incas. I remember using some
of these drawings in my book
"Atlantis: the Andes Solution".
I thought no more about it until recently, when I began to take more of an interest in Tiwanaku. First "Decoding the Tiwanaku Calendar" with a correct interpretation of the figures on the gate of the Sun and the relationship of the solar calendar to the 2 x 20 month lunar calendars at Tiwanaku.
The more I see of Tiwanaku, the more I am amazed by it. George Squier visiting the site in 1851 described "doric pillars" and even gave an illustration of one in his book "PERU Incidents of Travel and Exploration in the LAND OF THE INCAS" by E. George Squier, New York, Harper and Brothers, 1877.

Above, Tiwanaku pillar by George Squier 1851
I had not previously heard of pillars at Tiwanaku, and although I had visited the local church at the village of Tiwanaku, I had not thought of the pillars at the entrance to the church, which appear to be the ones removed from Tiwanaku.

Above, columns built into the entrance to the church at Tiwanaku.
What is remarkable about these pillars is that they are described as Doric pillars, meaning they are similar to a Greek order of architecture, but in fact they are also similar to a Persian order of architecture such as seen at the Temple of Anahita built by Ardeshir II (Artaxerxes II) around 404 to 359BC and located between Tehran and Kermanshah. They are also similar to pillars from the most ancient city of Susa, also today in Iran.

Above, columns from the Temple of Anahita, Iran
It would not be a surprise to find a Sumerian connection at Tiwanaku, after all George Squier describes the little figures called Chasquis on the Gate of the Sun as being in rows 8" high and 8" in Sumerian units would be 12 Sumerian shusi, also known as a "link". Moreover the standard size of an "Inca" adobe brick was 8" x 8" x 32" which would make it 12 x 12 x 48 shusi and numerous other examples of "Sumerian" measurements are found at Tiwanaku, not forgetting of course the "Fuente Magna" bowl which also has "proto cuneiform" writing and was found near Lake Titicaca.
A program recently broadcast on UK TV explained how the Viking conquerors of Ireland produced an illustrated book which purported to portray the native Irish as barbaric savages in order to fully justify their conquest and take-over of the country.
I am instantly reminded of the process which happened in Peru and Bolivia, not only was the country taken over and "colonised" but all trace of the civilised works of the original inhabitans was obliterated for the same purpose, to try and justify what was also considered an illegal act at the time it happened, and could only be justified if the natives were proven to be ignorant savages.
So in the end, the great city of Tiwanaku was literally smashed into thousands of pieces, some were used in the construction of the local church, some were used to adorn peasants' houses and the majority were carted off to build the city and cathedrals of La Paz. What remained was reduced even further by being broken into tiny pieces and used as ballast for the construction of the railway line. Unbelievable isn't it? But true. That is why there is so little remaining for the visitor to see today at Tiwanaku. And when you don't see great pyramids and great constructions, you don't imagine that here was the seat of a great empire or a great civilisation. But the evidence of the Tiwanaku calendar shows that this was indeed a remarkable and mathematically advanced civilisation, with a calendar based on 20's.
The Inca were a later people, sometimes it is said that they had writing on parchment but it was destroyed and forbidden upon the orders of one of the Incas having been advised to do so by the priests. They had a system of people especially trained to remember history and also used a system of devices called Quipus which used positional knots on strings to record numbers, and some say, it may even have been a language as well. But these specially trained people were also murdered to stamp out the use of these devices and help impose the catholic religion upon the people.
A calendar based on 20's was documented by parish priest Doctor Jose Domingo Duquesne in Columbia in 1795 in his "Disertacion sobre el calendario de los muyscas, indios naturales de este nuevo Reino de Granada", (Dissertation on the calendar of the Muyscas, natural Indians of this New Kingdom of Granada). Duquesne claimed that the Indians had a written system of symbols for numbers from one to twenty and provided a list of their names, (1) Ata (2) Bosa (3) Mica (4) Muihica (5) Hisca (6) Ta (7) Cuhupcua (8) Suhusa (9) Aca (10) Ubchihica (11) Quihicha Ata (12) Quihicha Bosa (13) Quihicha Mica (14) Quihicha Muihica (15) Quihicha Hisca (16) Quihicha Ta (17) Quihicha Cuhupcua (18) Quihicha Suhusa (19) Quihicha Aca (20) Quihicha Ubchihica.
The term gueta was also used to express the number twenty and the number forty was called guebo3ha, meaning, that is, two twenties.
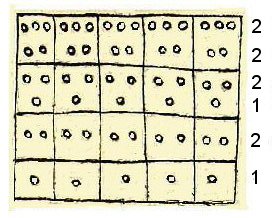
So we come to a picture of a quipu in Poma's book, along with a little box showing what we would assume is the code on how to operate the quipu.

Above, illustration of a quipu and the code to reading the quipu, from Guaman de Poma
Some people call the tablet with holes a Yupana, an early form of counting or calculating device.
I have seen this drawing a few times, and often wondered about the meaning of the coding, after all, it says contador meaning "counter" in the lower right hand corner of the page. At first sight, it seems a strange system since looking at the dots, counting from the right hand side you get on the top and on each row, heading towards the left, one, two, three and five. What happened to four? Or there again, if each dot represented five, then it would be five, ten, fifteen and twenty-five, again, what happened to twenty?
An enlargement of the code may provide the answer. They are not simply dots, they are positional mathematics very similar to the binary system used today and which I remember using back in the days of using punched paper tape to program computers. It is the enlargement which shows that some holes are filled in, and others left empty.
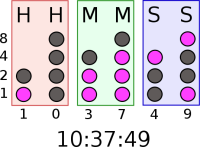
Above, example of code for a binary clock, source,
wikipedia

Above, enlargement of the Poma code

Above, enlargement of the code cleaned up
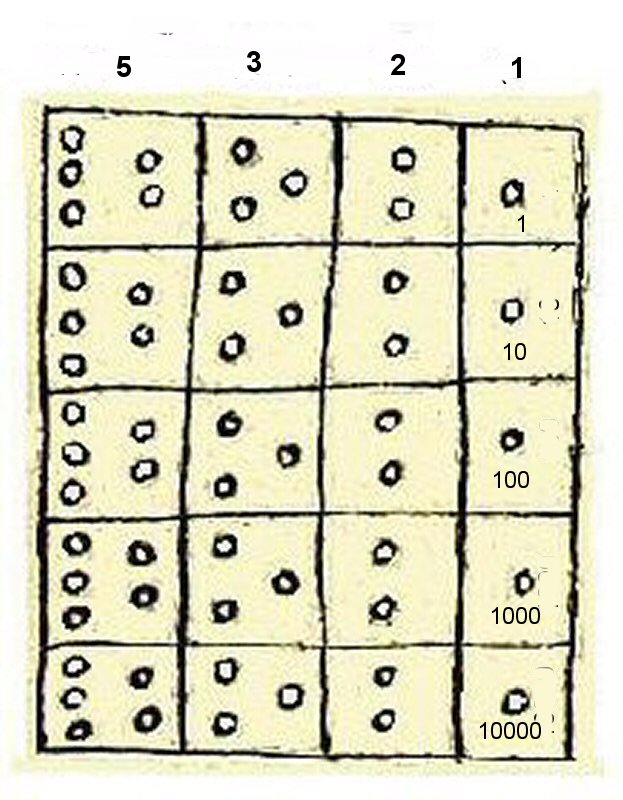
Above, an example of atributing simple decimal values to the panel,
if each hole had a value of 1, then each row would be 5 + 3 + 2 + 1 = 11 maximum.
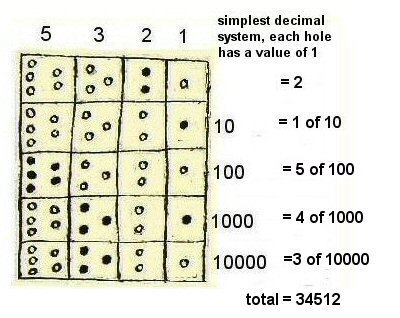
Above, simple version based on 10

Above, simple version based on 10
Easier to read in decimal system and horizontal format.
Above, simple version based on 10
Easier to read in decimal system and horizontal format.
At the time of the Conquest, the Incas counted by tens leading some people to believe the Yupana was based on a count of 10.
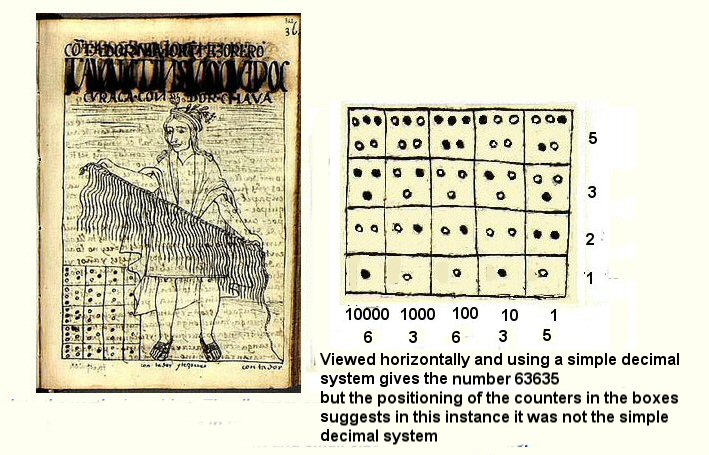
But the use of different squares in the Poma illustration suggests that in that example, the first row had a number greater than 10.

Above, base 40 system based on the values of the box, does not easily convert to decimal
If each hole had the value shown in the box above, then each square would have a maximum value of 5 x 5 + 3 x 3 + 2 x 2 + 1 + = 39
which might be good for a system counting in multiples of 40. At Tiwanaku, the calendar
counted in multiples of 20 for the solar year
and multiples of 40 for the lunar months.
But the Poma illustration appears to use a more sophisticated system than this and based upon multiples of 20.
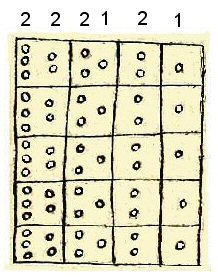
Above, enlargement of the code with potential values attributed to each hole
on the top row
that is, each hole individually has the value shown at the top
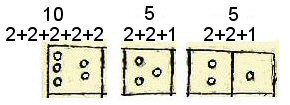
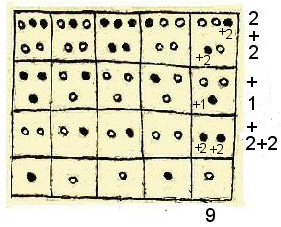
Above, the attributed values reveal a vigesimal system adding up to a maximum of 20 in the first row
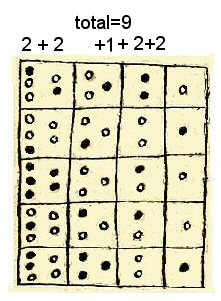
Above, in the first row, the dots add up to nine
Now may be a time to introduce a tablet said to be found at Tiwanaku.


Above, the symbols are very similar and suggest it may be easier for us to count
with the device in a horiontal position. We can also note the device has a small
animal figure with a hole for chain or cord both on upper and also on
the left hand side, suggesting the system could be read either horizontally or vertically.
Also, if this system belongs to Tiwanaku, then its origin is much much older than
the Incas
Above, the quipu code re-arranged in a horizontal posiiton.
Above, the first row still adds up to 9.
Above, the potential values of each box.
For the lower horizontal row
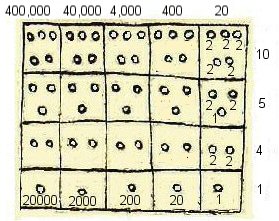
reading to the left we could choose multiples of 10 x 10 which would make a more simple decimal system giving 1, 10, 100, 1000, 10,000 and only require 3 horizontal rows,
or multiples of 20 x 20 giving very large numbers such as the Aztecs and Mayans used e.g. 1, 20, 400, 8,000, 160,000,
or multiples of 20 x 10 with 4 horizontal rows using 1, 20, 200, 2,000, 20,000 which makes a relatively simple system to operate.
Within the tablet, these become multiplied by the base value as indicated in
the right hand vertical row,
each vertical row has a mimium value as shown at the base of each column
and a maximum value as shown at the top of each column.

Above, the potential values of each box using a base line of 1, 10, 100, 1,000, 10,000.
It could function as a decimal calculator with only the three lower horizontal rows,
but as shown here would make a good mix of vigesimal and decimal system.
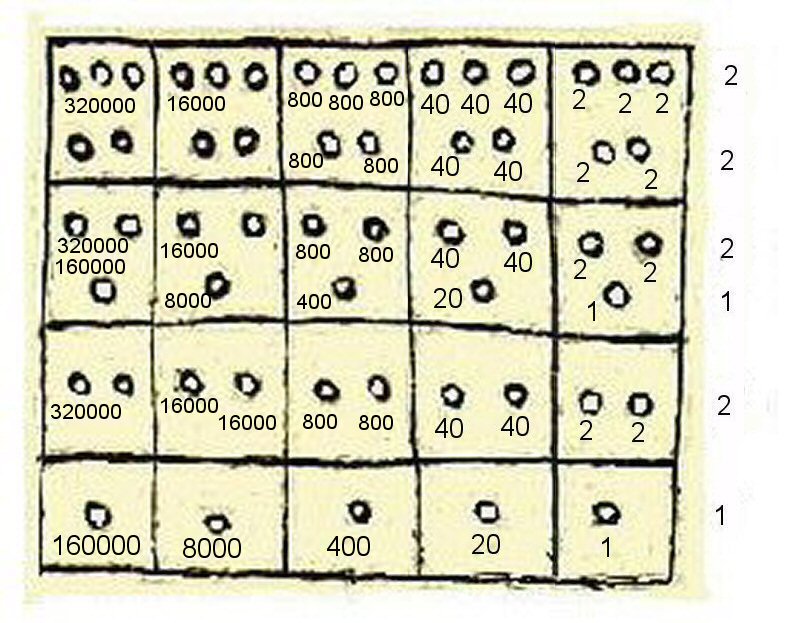
Above, the potential values of each box using a base line of 1, 20, 400, 8,000, 160,000.
This fits in well with the Aztec and Mayan mathematical systems used for manipulation of extremely large numbers
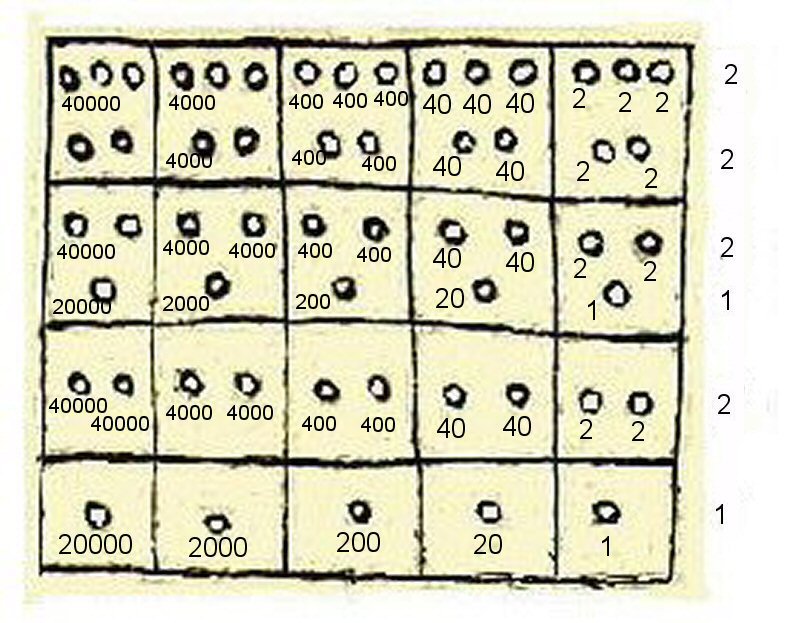
Above, the potential values of each box using a base line of 1, 20, 200, 2,000, 20,000.
This fits in well with the Tiwanaku calendar which in addition to a solar year, also used a "Zocam" year of
20 sidereal lunar months and an "Acrotom" year which equalled 2 x 20 i.e. 40 sidereal lunar months (being the same as 37 "Acrotom" synodic months) which
= 3 x solar years and every 400 sidereal lunar months an extra month was added to the calendar
to keep it synchronised with the solar year. So this seems more likely as the system used at Tiwanaku.
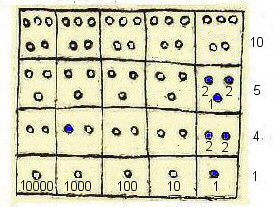
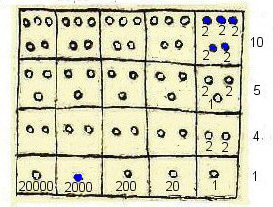
Above, the potential values of each box. Left, with a base 10 and right with a base 20
Example, today's date is year 2010.

Above, back to the vertical position, the potential values of each box.
Example, today's date is said to be year 5518 in the Aymara calendar.
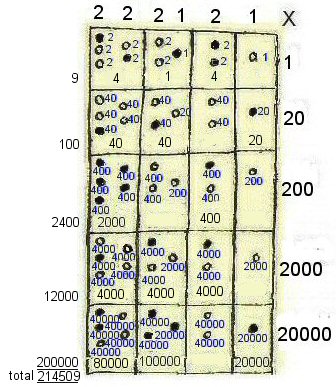
Back to the vertical position. The potential value of each individual hole
is shown and the marked value of each box is also shown.

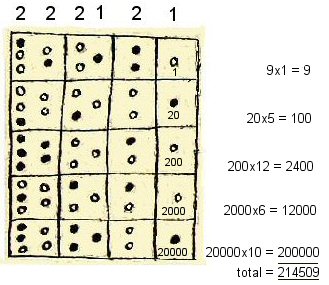
Back to the vertical position. The diagram on the right is based on the
parchment illustration -
the actual positions in the original holes is not very clear due to smudging
of the document and small size of original graphic.


This time the interpretation on the right uses columns based on 10 instead of 20.
We in modern times are trained to count on a decimal system using Arabic symbols for numbers
and naturally try to convert this system into something we can more easily understand
but the ancient Peruvians had no need to try and convert to our system.
The tablet has been described as "In the lower left corner, there is an abacus counting device used with maize kernels on which computations were performed and later transferred to the quipu. The maize kernels are the first numbers of the Fibonacci series, in which each number is a sum of two previous: 1, 2, 3, 5." But from the analysis above, it would seem that the tablet reveals a more sophisticated mathematical system than just a mere demonstration of the Fibonacci series, and could yet provide a key to a missing written or encoded language of the quipus.

There is another device found in Peru and said to be a calculating device. It is called a Yupana and various theories have been put forward as to how it funcioned.
The 16th-century account of Spanish priest José de Acosta suggests that Incas may have possessed such a device:
"To see them use another kind of calculator, with maize kernels. In order to carry out
a very difficult computation for which an able computer would require pen and paper,
these Indians make use of their kernels. They place one here, three somewhere else and eight.
They move one kernel here and there and the fact is that they are able to complete their computation
without making the smallest mistake. As a matter of fact, they are better at practical arithmetic than
we are with pen and ink. Whether this is not ingenious and whether these people are wild animals let
those judge who will! What I consider as certain is that in what they undertake to do they are superior to us."

Above, a yupana, It appears to be a different system to that shown
on the Poma drawing
and I would suggest the following may be how it would work,
using in this instance the decimal system.

Above, we can ascribe potential values to the boxes

Above, each box can contain nuts, beans, kernals, or anything similar which we can use as counters
and each counter accumulated in the individual boxes will have the values shown above.


Say we wish to multiply 21 x 36,
above left, we could choose to put the multiplier 36 in the left hand column, the subject, 21 in the lower row and find the answer accumulated in the right hand row.
Or above right, we could arrange our multiplier 36 in the left hand column and the subject, 21 in the right hand column and find the answer accumulated in the lower row.

To multiply 21 x 36, what we are doing is adding 21 to itself 36 times.

Step 1, add 2 and 1 buttons to the lower tray and to keep a record of the process, remove 1 button from the left hand column and store in the central left hand rectangular compartment.

Step 2, add 2 and 1 buttons to the lower tray and to keep a record of the process, remove
1 button from the left hand column and store in the central left hand rectangular compartment. We now have a running total of 42.

Step 3, add 2 and 1 buttons to the lower tray and to keep a record of the process, remove
1 button from the left hand column and store in the central left hand rectangular compartment.
We now have a running total of 63.

Step 4, add 2 and 1 buttons to the lower tray and to keep a record of the process, remove
1 button from the left hand column and store in the central left hand rectangular compartment.
We now have a running total of 84.

Step 5, add 2 and 1 buttons to the lower tray and to keep a record of the process, remove
1 button from the left hand column and store in the central left hand rectangular compartment.
We now have a running total of 105. We have also filled the tens compartment so.....

Step 5b, we adjust the compartments by removing the 10 buttons from the tens compartment, add 1
button to the hundreds compartment and store the surplus buttons in the right hand rectangular storage tray.
We still have a running total of 105.

Step 6, to complete this round, add 2 and 1 buttons to the lower tray
and to keep a record of the process, remove
1 button from the left hand column and store in the central left hand rectangular compartment.
We now have a running total of 126.

Step 7, we now do the multiplication of the tens,
add 2 and 1 buttons to the lower tray but this time add them one compartment to the left so that the 2 is added to the "hundreds" box and the 1 is added to the "tens" box...
To keep a record of the process, remove
1 button from the left hand column "tens" box and store in the central left hand rectangular compartment.
We now have a running total of 336.

Step 8, we continue the multiplication of the tens,
add 2 and 1 buttons to the lower tray again so that the 2 is added to the "hundreds" box and the 1 is added to the "tens" box...
To keep a record of the process, remove
1 button from the left hand column "tens" box and store in the central left hand rectangular compartment.
We now have a running total of 546.

Step 8, to complete the multiplication,
add 2 and 1 buttons to the lower tray again so that the 2 is added to the "hundreds" box and the 1 is added to the "tens" box...
To keep a record of the process, remove the last
1 button from the left hand column "tens" box and store in the central left hand rectangular compartment.
We now have a completed total of 756 showing that 36 x 21 = 756.

Above, yupana animation 36 x 21

There are a variety of ways in which the Yupana can be used.
All the counters can be of the same colour such as the earlier examples, or different colours
can be given different values as shown above.

In this example I have used different colours for the different values
as shown above. The small
compartments around the exterior are used for the actual calculations, while spare
counters can be kept in the right hand central storage compartments and
used counters from the left hand column in the left hand central storage compartments.

In this example I am using a using black beans for the subject number,
red for the multiplier and yellow for the
computation and answer number.

Above, we can try a simple multiplication, 134 x 235,
these numbers are represented by
kernels in the boxes.
We do this by a process of repetetive addition.
We now continue the multiplication by adding the number 134 three more times
to satisfy the 3 x 10's seen in the left hand column, this time adding the kernels one box higher up on the right hand column, just like we would using pen and paper (see below)
only two stages left to continue the multiplication by adding the number 134 twice more
to satisfy the 2 x 100's seen in the left hand column, again adding the kernels one box higher up on the right hand column.
In this example I am adding the
kernals in the right hand column
and the answer will be the total in the right hand column

Step 1 above, for the first addition we add the subject number, in this case, 134, to the right hand
column
and remove 1
kernel from
the left hand column and store in the left hand central tray.


Step 2 above, for the second addition we again add the subject number, another 134,
to the right hand column, that is, we add 4 kernals to the "ones" box so it now contains 8 "ones", 3 kernals to the "tens"
box so it contains 6 "tens" and 1 kernal to the "hundreds" box making 2 hundreds
and remove
1 kernel from
the left hand column making 2 stored in the left hand central tray.
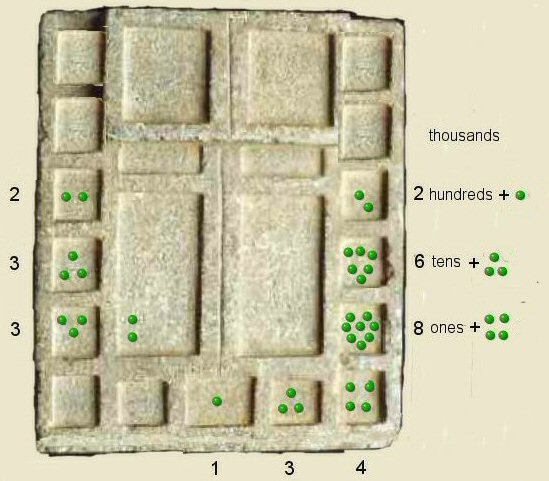
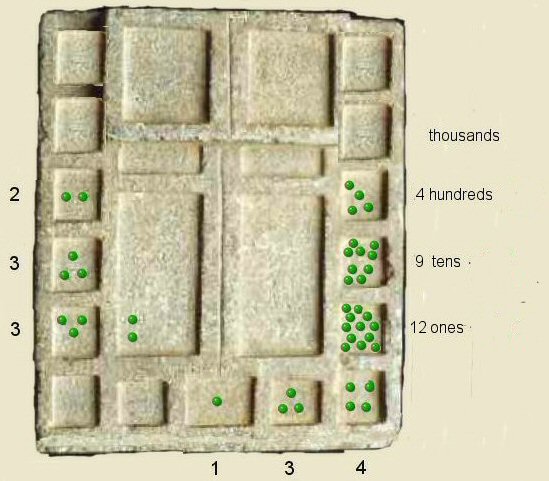
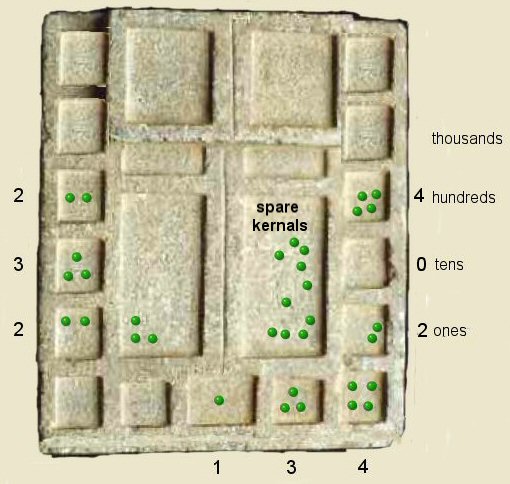
Step 3 above, for the third addition we again add the subject number to the right hand column,
in the "ones" box, four kernels were added to the eight kernels already there making 12 kernels, that is, 12 "ones".
As this would make the box full up and it would also exceed the base 10, we can remove
ten kernals and store them in the right hand rectangular centre box which is the spare kernals box and add
one extra kernal representing 10 to the box above, and if that now exceeds ten kernals
we similarly can remove ten from that box and add one to the box above it.
Whenever a box contains ten or more kernals we remove the extra kernals and add one to the box above,
and if that exceeds ten, we add the extra from that box to the one above and so on.
Two kernels are now left in the "ones" box and
the surplus kernels stored in the right hand rectangular centre box. The next box above (the tens)
contained the
six original kernals plus one carried over, to which were added three kernals from this addition,
making 10 kernals alltogether. Having reached 10 kernels, the box was emptied, 1 kernel added to the box above
and the surplus kernels stored in the right hand rectangular centre box.
We then had two kernels in the upper right hand box plus the one kernal carried
over to which was added the one kernal from this round of addition making four kernels in the upper right hand box.
To mark this round of addition, 1 kernel is removed from
the left hand column making 3 stored in the left hand central tray.
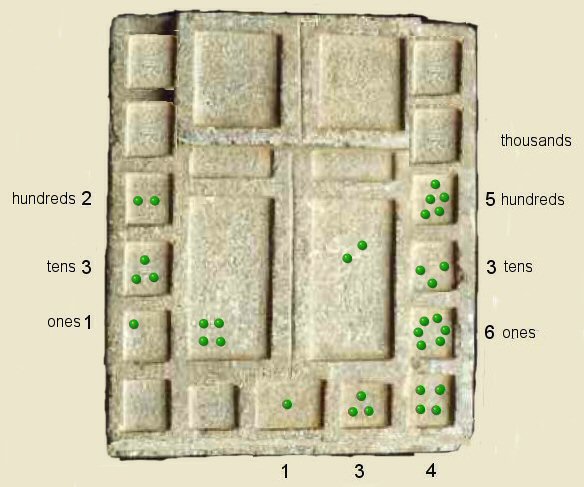
step 4 above, for the fourth addition we repeat the addition of the number 134
adding 4 kernels to the right hand column's lower box, three to the one above and one to the upper box
and take 1 kernel from the left hand column and store in left hand rectangular tray.
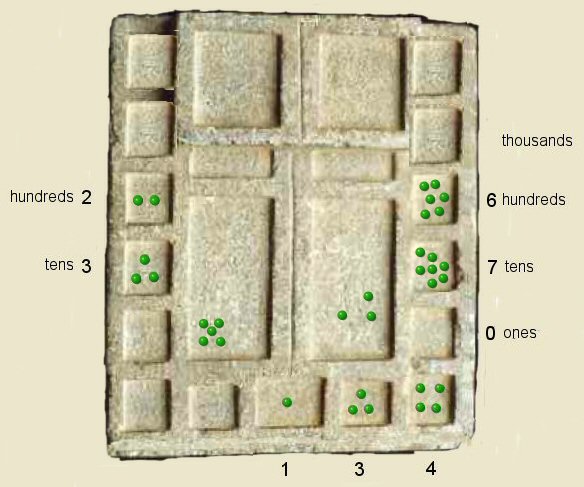
Step 5 above, for the fourth addition we again repeat the addition of the number 134
adding 4 kernels to the right hand column's lower box, this made 10 kernals in the
box so 10 were removed and 1 added to the box above etc, making a running total of 4, to this were added
three for this round of calculation making a total of 7 and one was added to the hundreds box making a running total of 670 in the right hand column.
To mark this round of computation we take the remaining 1 kernel from the left hand column
and store in left hand rectangular tray.
We have now completed this phase of the computation giving us a running total of 670 in the right hand column.

Above, how we would do it with pen and paper
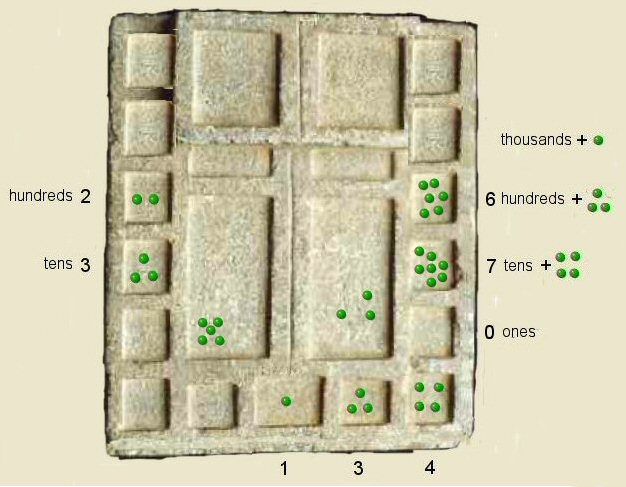
Step 6 above, for the addition of the tens, 1 and 3 and 4 kernals are added to the right hand column
but this time one level higher up.
This brings the running total into the thousands with two kernels in the thousands box of the right hand column.
To mark this round we take 1 kernel from the left hand tens box and store in left hand rectangular tray.

Step 7 above, 1 and 3 and 4 kernals are again added at this higher level, we
have now acquired three kernels in the thousands box of the right hand column,
to mark this round we
take 1 more kernel from the left hand tens column and store in left hand rectangular tray.
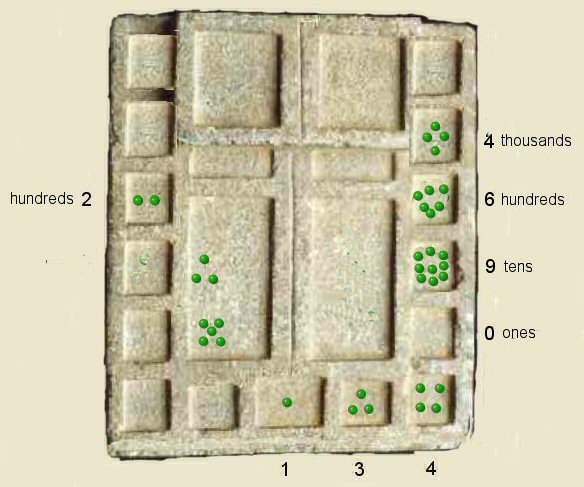
Step 8 above, on completion of this round, we have now acquired four kernels in
the thousands box of the right hand column giving a running total of 4690
and used up all the tens from the left hand column, storing the used kernals in the rectangular box.

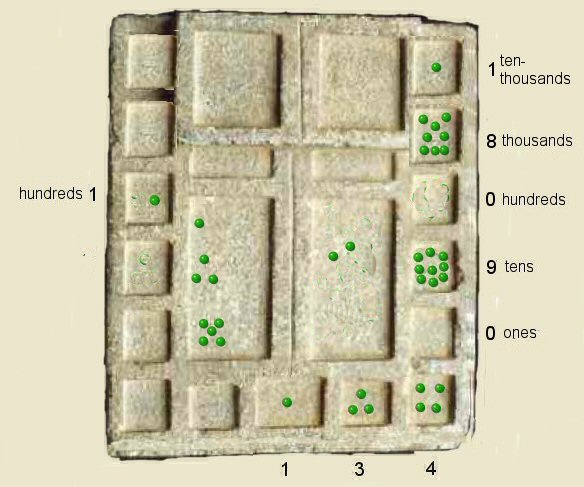
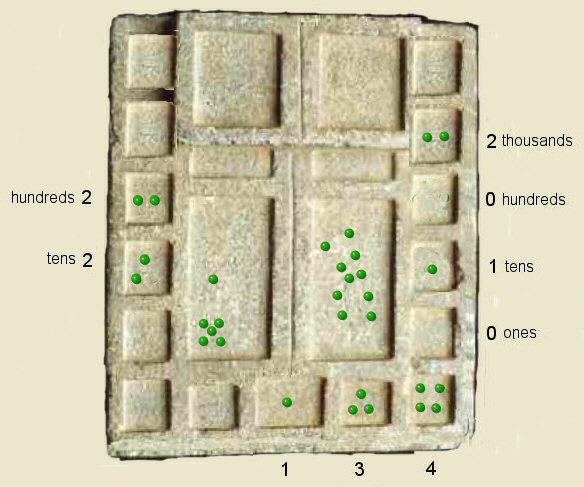
Step 9 above, 1 and 3 and 4 are again added to the right hand column, again one row higher up.
This brings the running total into the ten-thousands box,
we have now aquired eight kernels in the thousands box of the right hand column, zero hundreds, nine tens and zero ones making a running total of 18090.
We remove one of the kernals from the left hand column and store in centre box.
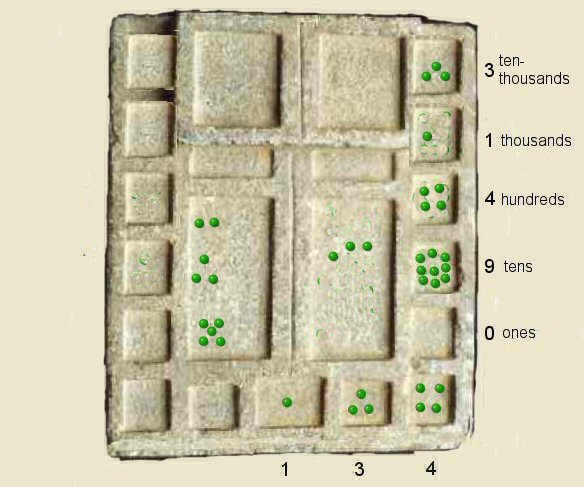
Step 10 above, we complete the equation by adding 1 and 3 and 4 kernals at this higher level
and find the total to be 31490,
and used all the kernels from the left hand column.

Above, yupana animation.
author
Atlantis: the Andes Solution (Atlantida: la solucion andina)
The Atlantis Trail (La Ruta de la Atlantida)
Atlantis: Lost Kingdom of the Andes (Atlantida, Reino Perdido de los Andes)
Atlantis and the Persian Empire
Tiwanaku: a city lost in time
Decoding Ezekiel's Temple
Decoding the Tiwanaku Calendar (descifrando el calendario tiwanaku)
bookstore

atlantisbolivia.org
webpage compiled 11 August 2010
webatlantis@hotmail.com